Die Zahlensysteme
Nicht selten muss ein Netzwerk umgeplant oder neu geplant werden, wenn neue Endgeräte in ein Firmennetzwerk eingebunden werden. Im Mittelpunkt stehen hierbei die unvermeidlichen verschiedenen Zahlensysteme.
Da die Kommunikation zwischen den Hosts und den Server(n) sicher gestellt werden müssen, dürfen hier keine Fehler passieren. Jeder Netzwerkadministrator muss die folgenden Umrechnungen von Zahlensysteme verstehen und beherrschen, um den Aufbau von Netzwerken über Subnetmasken bzw. IP-Adressen nachzuvollziehen.
- Binäres-System (2'er)
- Dezimal-System (10'er)
- Hexadezimal-System (16'er)
Aufgrund des modernen Zeitalters sind bereits viele technische Unterstützungsmöglichkeiten wie App's fürs Handy oder professionelle Netzwerksoftware aus dem Boden gewachsen, mit der sich z.B. Teilnetze, Adressbereiche und Zahlensysteme errechnen lassen. Dennoch sollte man es nicht aus dem Auge verlieren, sich mit den manuellen Berechnungen auseinander zu setzen.
In diesen Beitrag werden die verschiedenen Umrechnungen leicht verständlich dargestellt.
Das Binär-System
Umrechnung Binär in Dezimal
Umrechnung Binär in Hexadezimal
Das Dezimal-System
Umrechnung Dezimal in Binär
Umrechnung Dezimal in Hexadezimal
Das Hexadezimal-System
Umrechnung Hexadezimal in Binär
Umrechnung Hexadezimal in Dezimal
Das Binär-System
Das Binär-System auch Dual-System oder auch 2'er System genannt, besteht aus einem Zeichenvorrat von 2 Zeichen.
Zeichenvorrat: (2 Zeichen): 0, 1
Umrechnung von Binär in Dezimal
Binärzahl: 10011010
Wir zählen anhand des Stellenwerts nur die Zahlen zusammen die in der Binärzahl eine 1 anzeigt.
(..., 4096, 2048, 1024, 512, 256, 128, 64, 32, 16, 8, 4, 2, 1)
Binärzahl: 1 0 0 1 1 0 1 0
Stellenwert: 128 64 32 16 8 4 2 1
Ergebnis: 128 + 16 + 8 + 2 = 154
Umrechnung von Binär in Hexadezimal
Binärzahl: 10011010
Zeichenvorrat Hexadezimal (16 Zeichen): 0,1,2,3,4,5,6,7,8,9, 10=A, 11=B, 12=C, 13=D, 14=E, 15=F
Wir teilen die Zahl in 4'er Blöcke auf.
1001 1010
Wir fangen rechts an.
Wir zählen anhand des Stellenwerts (8, 4, 2, 1) nur die Zahlen zusammen die in der Binärzahl eine 1 anzeigt.
Binärzahl: 1 0 0 1 1 0 1 0
Stellenwert: 8 4 2 1 8 4 2 1
- Wir beginnen mit dem rechten 4'er Zahlenblock 1010 (2+8) = 10 (10 = A)
- Wir machen mit dem zweiten Zahlenblock von rechts weiter 1001 (1+8) = 9
Ergebnis: 9A
Dezimal-System
Das Dezimal-System auch 10'er-System genannt, besteht aus aus einem Zeichenvorrat von 10 Zeichen.
Zeichenvorrat (10 Zeichen): 0,1,2,3,4,5,6,7,8,9
Umrechnung Dezimal in Binär
Binär-Zeichenvorrat: (2 Zeichen): 0,1
Beispiel (Zahlen bis 255)
Dezimalzahl 154 in eine Binärzahl umrechnen.
Diese Umrechnung eignet sich gut, wenn man schnell ohne Taschenrechner IP-Adressen (8 Bit) umrechnen möchte.
Jetzt ist ein wenig Kopfrechnen angesagt.
Wir nutzen dazu folgende Stellenwerte (8 Bits: 128, 64, 32, 16, 8, 4, 2, 1)
Es wird nur überprüft, ob die jeweilige Zahl (Bit) in die Dezimalzahl passt.
Ja = 1;
Nein = 0;
Bei "Ja" notieren wir eine 1 und merken uns den Rest, mit den wir dann weiter rechnen. So lange bis 0 erreicht ist.
Passt 128 (Bit) in 154 = 1 Rest = 26
Passt 64 (Bit) in 26 = 0
Passt 32 (Bit) in 26 = 0
Passt 16 (Bit) in 26 = 1 Rest = 10
Passt 8 (Bit) in 10 = 1 Rest = 2
Passt 4 (Bit) in 2 = 0
Passt 2 (Bit) in 2 = 1 Rest = 0
Passt 1 (Bit) in 0 = 0
Ergebnis: 1001 1010 (von oben nach unten)
Umrechnung Dezimal in Hexadezimal
Hex-Zeichenvorrat: 0,1,2,3,4,5,6,7,8,9, 10=A, 11=B, 12=C, 13=D, 14=E, 15=F; (16 Zeichen)
Beispiel 1
Umrechnung einer Dezimalzahl 2016 in eine Hexadezimalzahl.
Hierzu muss nur die Dezimalzahl durch den Wert 16 geteilt werden.
Bei dem Ergebnis wird nur mit der Ganzzahl weiter gerechnet, die wiederum durch 16 geteilt wird.
2016 : 16 = 126 (Rest 0) | Rechnung geht auf.
126 : 16 = 7 (Rest 14=E) | 16*7=112; 126-112=14
7 : 16 = 0 (Rest 7) | 7 bleibt über (16 passt nicht in 7)
Ergebnis: 7E0
Beispiel 2
Dezimalzahl 100 in eine Hexadezimalzahl.
100 : 16 = 6 (Rest 4) | 16*6=96; 100-96=4;
Ergebnis: 64
Beispiel 3
Dezimalzahl 90 in eine Hexadezimalzahl.
90 : 16 = 5 (Rest 10) 10 = A | 16*5=80; 90-80=10;
Ergebnis: 5A
Hexadezimalsystem
Das Hexadezimal-System auch 16'er-System genannt, besteht aus einem Zeichenvorrat von 16 Zeichen, wobei die Null auch mitgezählt wird.
0,1,2,3,4,5,6,7,8,9;
Die Zahlen 10,11,12,13,14,15 werden durch Buchstaben von A-F ersetzt.
A steht für 10,
B steht für 11,
C steht für 12,
D steht für 13,
E steht für 14,
F steht für 15;
Zeichenvorrat: 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F; (16 Zeichen)
Beispiel für Hexadezimalzahlen
8A, 11B, 3AF, 5BE3;
Umrechnung Hexadezimal in Binär
Die Umrechnung erfolgt in 2 Schritten
- Vom Hexadezimal-System in das Dezimal-System (10'er) umrechnen.
- Vom Dezimal-System (10'er) in das Binär-System (2'er) umrechnen.
Schritt 1
Umrechnung einer Hexadezimalzahl 20FA in eine Dezimalzahl.
Hierbei verwenden wir die Potenz von 16.
Die 2 und die 0 bleiben als Zahl bestehen.
Das F = 15 und das A = 10.
(2 x 163) + (0 x 162) + (15 x 161) + (10 x 160)
8192 + 0 + 240 + 10
8192 + 250
8442
Schritt 2
Umrechnung der Dezimalzahl 8442 in eine Binärzahl.
Wir teilen den Wert und anschließend den Rest (Nur die Ganzzahl) solange durch 2 bis keine Zahl mehr zum teilen übrig ist.
Ergebnis mit Rest = 1;
Ergebnis ohne Rest = 0;
8442 : 2 = 4221; Rest = 0
4221 : 2 = 2110; Rest = 1
2110 : 2 = 1055; Rest = 0
1055 : 2 = 527; Rest = 1
527 : 2 = 263; Rest = 1
263 : 2 = 131; Rest = 1
131 : 2 = 65; Rest = 1
65 : 2 = 32; Rest = 1
32 : 2 = 16; Rest = 0
16 : 2 = 8; Rest = 0
8 : 2 = 4; Rest = 0
4 : 2 = 2; Rest = 0
2 : 2 = 1; Rest = 0
1 : 2 = 1; Rest = 1
Ergebnis: 0010 0000 1111 1010 (von unten nach oben)
(Fehlende Stellen beim linken 4'er Block werden mit Nullen aufgefüllt!)
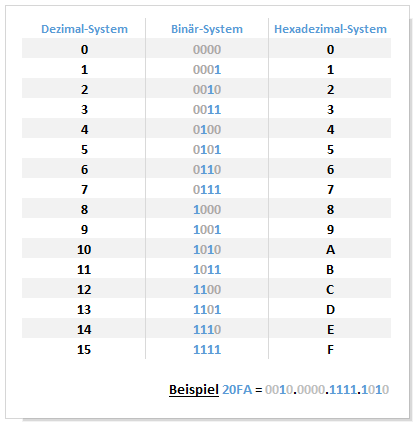
Umrechnung Hexadezimal in Dezimal
Beispiel 1
Umrechnung einer Hexadezimalzahl 8A in eine Dezimalzahl.
Hierbei verwenden wir die Potenz von 16.
Die 8 bleibt als Zahl bestehen.
Das A als Zahl ist 10.
(8 x 161) + (10 x 160)
128 + 10
138
Beispiel 2
Umrechnung einer Hexadezimalzahl 20FA in eine Dezimalzahl.
Hierbei verwenden wir wieder die Potenz von 16.
Die 2 und die 0 bleiben als Zahl bestehen.
Das F = 15 und das A = 10.
(2 x 163) + (0 x 162) + (15 x 161) + (10 x 160)
8192 + 0 + 240 + 10
8192 + 250
8442
Weitere Informationen
Um die Umrechnung vom Binär-System in das Hexadezimal-System anhand eines Videos zu vertiefen, gibt es hier ein hervorragendes Video zum Hexadezimalsystem
