Hexadezimalsystem

Das Hexadezimal-System auch 16'er-System genannt, besteht aus einem Zeichenvorrat von 16 Zeichen, wobei die Null auch mitgezählt wird.

0,1,2,3,4,5,6,7,8,9;

Die Zahlen 10,11,12,13,14,15 werden durch Buchstaben von A-F ersetzt.
A steht für 10,
B steht für 11,
C steht für 12,
D steht für 13,
E steht für 14,
F steht für 15;

Zeichenvorrat: 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F; (16 Zeichen)

Beispiel für Hexadezimalzahlen

8A, 11B, 3AF, 5BE3;

Umrechnung Hexadezimal in Binär

Die Umrechnung erfolgt in 2 Schritten

1. Vom Hexadezimal-System in das Dezimal-System (10'er) umrechnen.
2. Vom Dezimal-System (10'er) in das Binär-System (2'er) umrechnen.

Schritt 1
Umrechnung einer Hexadezimalzahl 20FA in eine Dezimalzahl.
Hierbei verwenden wir die Potenz von 16.

Die 2 und die 0 bleiben als Zahl bestehen.
Das F = 15 und das A = 10.

(2 x 163) + (0 x 162) + (15 x 161) + (10 x 160)
  8192    +     0     +   240     +     10
         8192         +          250
                    8442

Schritt 2
Umrechnung der Dezimalzahl 8442 in eine Binärzahl.

Wir teilen den Wert und anschließend den Rest (Nur die Ganzzahl) solange durch 2 bis keine Zahl mehr zum teilen übrig ist.
Ergebnis mit Rest = 1;
Ergebnis ohne Rest = 0;

8442 : 2 = 4221; Rest = 0
4221 : 2 = 2110; Rest = 1
2110 : 2 = 1055; Rest = 0
1055 : 2 =  527; Rest = 1
 527 : 2 =  263; Rest = 1
 263 : 2 =  131; Rest = 1
 131 : 2 =   65; Rest = 1
  65 : 2 =   32; Rest = 1
  32 : 2 =   16; Rest = 0
  16 : 2 =    8; Rest = 0
   8 : 2 =    4; Rest = 0
   4 : 2 =    2; Rest = 0
   2 : 2 =    1; Rest = 0
   1 : 2 =    1; Rest = 1

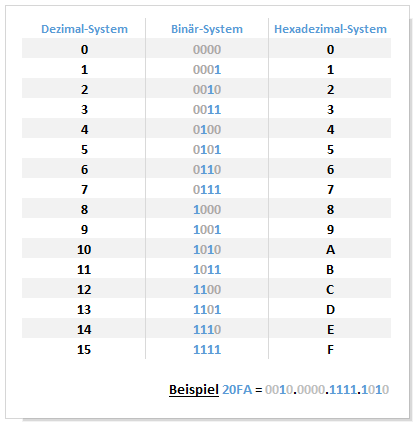
Ergebnis: 0010 0000 1111 1010 (von unten nach oben)
(Fehlende Stellen beim linken 4'er Block werden mit Nullen aufgefüllt!)

Umrechnung Hexadezimal in Dezimal

Beispiel 1

Umrechnung einer Hexadezimalzahl 8A in eine Dezimalzahl.
Hierbei verwenden wir die Potenz von 16.

Die 8 bleibt als Zahl bestehen.
Das A als Zahl ist 10.

(8 x 161) + (10 x 160)
   128    +     10
         138

Beispiel 2

Umrechnung einer Hexadezimalzahl 20FA in eine Dezimalzahl.
Hierbei verwenden wir wieder die Potenz von 16.

Die 2 und die 0 bleiben als Zahl bestehen.
Das F = 15 und das A = 10.

(2 x 163) + (0 x 162) + (15 x 161) + (10 x 160)
   8192   +    0     +    240     +     10
         8192        +           250
                    8442

Weitere Informationen

Um die Umrechnung vom Binär-System in das Hexadezimal-System anhand eines Videos zu vertiefen, gibt es hier ein hervorragendes Video zum Hexadezimalsystem